Claude Code to (my) exhaustion: a DP worklog

Recently at work I had a side quest on the following task: choose a binning scheme for some 1-dimensional data that has an annoying distribution. Quantile binning wasn't great (at the sparse tails it produces very wide bins, and in the center very tiny ones), and equal width was also out.

Basically I wanted to be able to specify a number of bins (n_bins) and get some "reasonable" bin edges out.

def compute_bin_edges(data: np.ndarray, n_bins: int) -> np.ndarray:
    ...

Well, one nice definition of "reasonable" is the Jenks natural breaks or Fishers natural breaks¹: pick the bins so that the within-bin variance is minimized. This method seems to be pretty widely used in mapping and visualization (especially GIS) libraries to try to divide datasets (e.g. color parts of a map). It was even featured in a ThePrimeagen video.

The core algorithm would make a nice dynamic programming homework problem:

Here's part of the solution (the DP definitions), hidden in case you want to try to think it through for yourself:

There are 3 clean ways ways to do this²:

1. A simple quadratic ($\mathcal{O}(k \cdot n^2)$) version that just takes advantage of optimal substructure (i.e. classic DP, no optimizations) (Jenks, 1977) .
2. A slightly more complicated log-linear variant ($\mathcal{O}(k \cdot n \log n)$) that also takes advantage of something called the concave Monge property (but is just a way to compute the DP matrices faster) (Wu, 1989) ³.
3. A shiny fast linear variant ($\mathcal{O}(k \cdot n)$) variant that uses a more complicated algorithm (SMAWK) to find the minima of the DP matrices (the goal) while computing only what's necessary (Wu, 1991) . Note that this is linear iff the input is sorted (for the rest of this we'll assume the data is pre-sorted). (Song, 2020) also implemented an in-place search space reduction (which to be honest was what I thought SMAWK was already doing).

To be clear there are plenty of packages to do this in Python already with good enough performance. There's also a very feature rich reference implementation by some of the authors of the 2020 paper in R/C++. But I was interested in learning about the linear algorithm⁴ and also interested in some extensions (adding min/max width constraints, $k$-medians, etc.), which I figured would be relatively easy once I had the core algorithm implemented.

So I figured, great task for Claude Code, right? This is:

1. A clear problem description with 3 variants that are pure functions all with the same API
2. At least the first two solutions are probably well represented in LLM training data
3. It's easy to generate more test data (random()!) and there is a unique correct solution for every input

Giving Claude context

Since there was a high quality reference implementation for these algorithms, I cloned the repository and giving it access to the code would be useful (I put this in a reference/ folder, and put directions in CLAUDE.md) I also downloaded several papers and put them in .tex and .pdf form into the repository: (Grønlund, 2017) , (Wu, 1991) , and (Aggarwal, 1987) .

Of course as usual I created a CLAUDE.md with plenty of detail and a TODO.md with an organized plan for implementation, which looked something like this:

1. Make really good test cases (i.e. test for degenerate distributions, really sparse in tails, really sparse in middle, etc.)
2. Implement the QUADRATIC algorithm, and for small test cases check it for correctness against a brute force version
3. Implement the LOGLINEAR algorithm and verify that it gives exactly the same result as the QUADRATIC
4. Implement the LINEAR algorithm and verify that it gives exactly the same results as the other two algorithms

Of course, I had implicit ideas about how this should be done, but I didn't manage to write this down in the TODO.md or background information. I mentioned that it would be great to implement this in Python + Numba to keep the final implementation readable / easy to change (Numba is fantastic these days). Unfortunately, in the CLAUDE.md I also described how I wanted to eventually add min/max_width constraints.

What went well

Claude was able to relatively quickly deliver working code for the core QUADRATIC and LOGLINEAR algorithms.

What was not so good

1. Claude read the reference code and saw a structure that switched based on user input between (QUADRATIC, LOGLINEAR, LINEAR) algorithms and also between $k$-means and $k$-medians, and it decided to mimic that structure (let's call it general_ckmeans). This overcomplicated the code early on (a lot of jumping between functions) and made it hard to read. I told it not to do that and asked for the 3 functions that I wanted implemented as separate interfaces.
2. Claude also saw code in the reference implementation that tried to estimate what the optimal n_bins was and implemented a LOT of new code related to that; this also overcomplicated the data flow a lot.
3. It generated test cases before doing the above (as I asked), but since it left general_ckmeans around, the tests were wired against the old implementations, so when it ran the tests, they passed (that was a correct implementation!). I realized that if you asked for n_bins that were more than the length of the data it returned essentially an error, so I explained what I wanted instead (adjust n_bins down / return fewer bins) and it added both a new test (as I explicitly asked) and the code changes, and it failed (still old implementation).
4. Claude decided to add min/max_width arguments to the implemenation while writing it (seeing my desire to do this later), but since it didn't see code to implement it in the reference implementation, it just ignored those arguments. It apparently added some test cases for those arguments, but then when those failed, it read its code, realized it was ignoring those arguments, and decided to silently make the tests pass "for now". Given that I wanted to do test-driven development, this was super frustrating.
5. I told Claude to never do that again (failing tests is ok unless the current goal is to solve that test specifically), and it made those tests actually run. However, my trust in Claude was shaken at this point so I checked the testcases - there are still some passing constraint-checking testcases. It turned out the passed min_width and max_width in those cases was just too lenient, so the optimal bins (without constraints) also passes.
6. I wanted a bit more confidence that these bin assignments were optimal, so I asked it to do an iterative refinement check, by basically wiggling a random bin edge until it changed an assignment, then checking if that assignment was better - essentially, are we at a local minimum? Claude added this test, but it took a while to explain what I wanted, and to verify that Claude did this correctly.
7. Claude decided around this point that it wanted to implement the min/max width constraints (I had added it to the TODO list at the end by this point) and it decided to do this by just wiggling the bin widths after optimization until they met the min/max constraints. It only did this if min/max bin width were passed, and since I didn't have a way to compute the optimal answer in that case, I didn't pass in min/max bin width in the first set of correctness tests. So it was giving incorrect results (a greedy approach like the above doesn't work), and I didn't know.
8. Eventually I noticed the constraint tests were re-activated and tried to investigate; I also expanded the local minima tests to include min/max width constraints, which promptly failed. Investigating led me to tell Claude to stop implementing min/max width constraints and delete the incorrect code.
9. At this point we're trying to implement the LINEAR variant. It tries for a second, decides it's too hard, and decides to implement an approximation (this decision happens in thinking but wasn't communicated to me). This was very frustrating and I ask it what context it needs to implement this correctly, and get those references (some of the papers, it needs some human description of what part of the reference codebase implements this, etc). Somewhere around here I reset the session and context.
10. It implements the LINEAR variant with a lot of guided help from me, e.g. telling it to check the computed cost/backtracking matrices against the LOGLINEAR variant (which we have to refactor to extract, etc.). I don't pay attention to details besides "is this implementing it the right way" because, frankly, the LINEAR algorithm is complex. Maybe the AI can do it for me. The only exception is when it started segfaulting, I told it to turn the recursive algorithm into an iterative one.
11. The local minima test cases are failing for the linear variant, which Claude eventually concludes is a "known issue" (what?). I ask it about this and it says "there's probably a subtle bug in these testcases". I ask it to check if the new bin assignment that is being generated from the tweaked bin edges is even different... it isn't. Since the cost function went down, that means the cost function is incorrect - I realize at this point that this whole set of testcases doesn't really work.
12. After some detailed directing, it makes those test cases correct again, and eventually makes the LINEAR testcases pass. Wow!

My overall feeling after this was basically that while you can use Claude or Copilot or Cursor to generate the tests the first time, it's probably best to think hard about it yourself afterwards, verify that it's the behavior you want, organize them by which TODOs will solve them, and then don't let Claude touch the tests. It is just so willing to silence failing tests "for now" and it really leads to confusion. I also think the bias towards "must solve testcases" is so strong that it will kind of jump ahead and solve them even if that's not the next task on the TODO.

Where I gave up

Right after the above series of steps I asked it to profile the runtimes of each algorithm. It produces some emoji-heavy slop that is impossible to read, so I manually clean up the profiling script. It was profiling including the sort, so I refactor the code to move that out of the core function that's profiled.

At this point I realize the runtime of the LINEAR variant is actually quadratic in the input (in fact, it's slower than the QUADRATIC). That's about where I gave up on Claude Code to get me farther.

Fixing the slop

Since Claude had implemented the LINEAR variant I kind of stubbornly stuck to that code for a while and tried to see if I can fix it, but since I didn't know the algorithm at all, I had no idea what was going on. It turns out that correctly implementing it in linear time is subtle, and I had just thrown some kind of rabid approximate LLM agent at it.

So I reached for tools from a more elegant age: I opened the 1987 paper (scanned pdf!). Even there I had "better" tools though than just reading it top to bottom - I asked o3 about the paper, what a totally monotone matrix was, intuition for the lemmas, etc.

Around this point I started to think about the tradeoffs of using an LLM and using my own brain. To be honest the time I spent asking o3 about this paper was nontrivial, and the paper is not that long. Maybe I'm saying this on the other side after figuring it out, but it felt like every time I was confused I would ask o3 some question, read the response, think about it, but because the "escape button" was so convenient, I never thought very hard. Eventually I stopped using o3 and actually thought about it, and it started to make sense.

Then I wrote a (hopefully) correct implemention in pure Python. This one scaled linearly in the number of accesses to the monotone matrix (a proxy for the runtime), so I spent a little bit of time optimizing it to remove unnecessary rows, wrap with nb.njit, etc. And voila! A fast "human crafted" implementation of the linear SMAWK algorithm.

After this I realized that there were many inconsistencies across the different algorithms (e.g. handling early exits, etc.) that made reading the code harder, so I cleaned that up. Claude could have probably done this, but I was tired of prompting by this point.

Was it worth it?

Vibe-coding right now is valuable to me because it helps me understand the limits and capabilities of coding LLMs (agents and tab-style assistants). So the exploration was worth it for that alone.

As a development assistant, the thing that strikes me is that I didn't really fully understand the algorithm until I stopped using LLMs at all, which is probably no surprise to anyone. And I think understanding was a prerequisite to finishing, trying to avoid that telling Claude to test X or Y or think harder was not productive. I was hoping that Claude was smarter than me and could present the idea in a nicer way than the paper via the code, but that wasn't really true.

Incidentally I built a lot of tools (careful reusable prompts) for reading/summarizing papers and guiding Claude towards test driven development, so that work might give returns into the future.

I was reading antirez's blog post and saw this:

[...] when left alone with nontrivial goals they tend to produce fragile code bases that are larger than needed, complex, full of local minima choices, suboptimal in many ways. Moreover they just fail completely when the task at hand is more complex than a given level.

Well, that's my experience. Even for very pure implementation goals, they're just very sloppy. The emojis in particular in my entire codebase drove me nuts (I eventually made a TODO to remove all emojis, which you can )

What's left with binning

shows a way to do the binning with the $k$-medians objective, and that's probably pretty easy to adapt (in practice this is a few lines change). I also want to implement min/max bin widths since practically speaking I need those for work.

A fun plot

As any student of computers knows, the "best" algorithm by big-$\mathcal{O}$ runtime is rarely (never?) the most useful, because of dumb "reality" like cache locality, aligned memory access, register pressure, etc.

In practice the LOGLINEAR algorithm is significantly better than the LINEAR algorithm, and you can barely feel the $\log n$ factor compared to the constant:

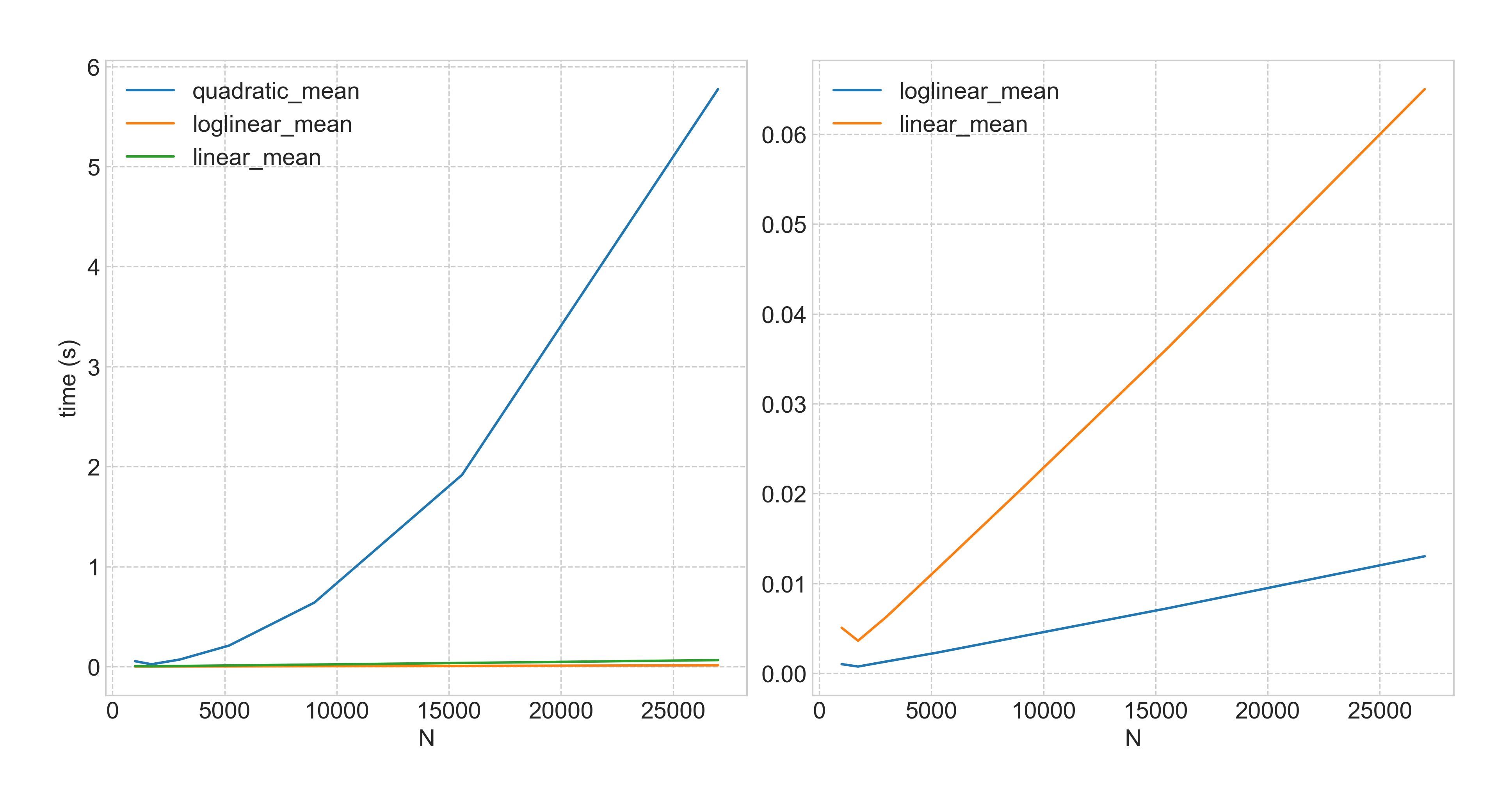
Check it out on Github!

Challenge

Someone out there is a better LLM whisperer than me. Do you have a prompt and environment for Claude that one-shots the 1D optimal breaks problem?